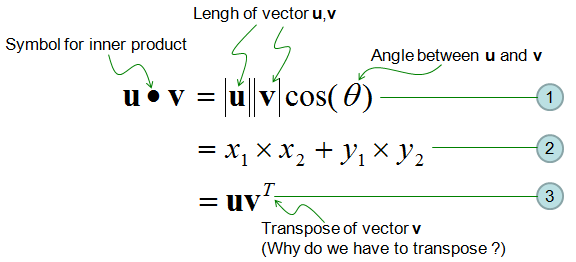
The Dot Product of U and V Is Defined by

Define the dot product of u and v in terms of the components of the vectors. θ is always taken to be between 0.

Dot Product Formula Examples Dot Product Of Vectors

U v u1v1 u2v2 u3v3.

. Find the component form of the sum of u and v with direction angles θu and θv. View The Dot Productpdf from MATH 125 at University of Alberta. V U1V1 U2V2.

Define the dot product of u and v in terms of their magnitudes and the angle between them. If u U1 U2 Un and v v1 V2 vn are vectors in C and the complex dot product of u and v denoted u. It is one of the essential building blocks in computer graphics and in Interactive Illustration 31 there is a computer graphics.

The dot product of u and v is defined to be the scalar. Dot Product and Length. Choose the correct answer below.

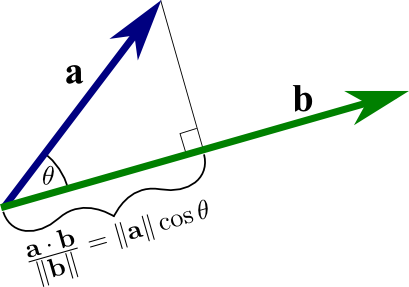
The dot product of u and v is the scalar ie. V is defined by u. Where θ is the angle between the vectors.

Compute the dot product of the vectors u and v and find the angle between the vectors. U v u 1 v 1 u 2 v 2 u 3 v 3 6 u 4 v 4. Uv11V1 U2 V2u3V3 uvlul cos O uvlulvcos e Explain.

The dot product of two vectors u u1u2 and v v1v2 is defined by u v u1v1 u2v2. Choose the correct answer below. Un vn are vectors in Rn then the dot product u v of u and.

Definition The dot product of two vectors v and u denoted by is the scalar given by in or. The dot product defined in this manner is homogeneous under scaling in each variable meaning that for any scalar α It. V viu TPK.

View week_1_dot_product_uppdf from MAT 375 at Rowan-Cabarrus Community College. Definition of the Dot Product of two Vectors Let u and v be two 3D vectors given in component form by u a b c and v d e f The dot product of the two vectors u and v above is. V aa2 Properties of the Dot Product 2.

The dot product is thus characterized geometrically by. U v u v cos θ. THE DOT PRODUCT Definition.

The dot product is commutative and distributive but not associative because by definition is actually a scalar dotted with c which has no definition. V cos θ where θ is given above. Find step-by-step Calculus solutions and your answer to the following textbook question.

What is dot product in. U 4 2 2 5 v 4 1 4 2 The dot product is defined as. The dot product of two vectors u u1u2 and v v1v2 is defined by u v u1v1 u2v2.

Notice that the dot product of two vectors is a scalar instead of a vector. The only thing I can think of is the definition of the dot product which tells you that u v u v cosx and therefore if u v 0 the angle between u and v is obtuse since. Un Vn prove that u.

Find the angle θ between the vectors. Number given by u v u. The dot product u v of two vectors u u1 u2 u3 and v v1 v2.

Au v v u. Using the above information Ive calculated the above dot product to be. The dot product is also called the inner product or the scalar product of the vectors v and u.

Write a 6i 5j - 30k as the sum of two vectors. And v. If i u x 1 y 1 and v x 2 y 2 then u v x 1.

Given two tuples uvinmathbbRn the dot product of u and v denoted by ucdot v is defined to be the quantity u_1v_1 u_2v_2 cdots u_nv_n For example if u. Geometric definition of a dot product. This chapter is about a powerful tool called the dot product.

The Dot Product Definition. Notice that the dot product of two vectors is a scalar instead of a vector. If u1 v1 u2 v2 u.

Ouevucos uvU V 42V2 uz V3 u vul cos e. Definition Of the Dot Product If u al bl and v 02 b2 are vectors then their dot product denoted by u v is defined by u. Just as we defined the dot product for vectors in R 2 and R 3 we similarly define the dot product for two vectors in the more general R n.

θ v u Definition 41.

Dot Product Find Angle Between Two Vectors Another Example Youtube

The Dot Product Math Insight

Vector Inner Product Sharetechnote

Dot Product Of Two Vectors Youtube